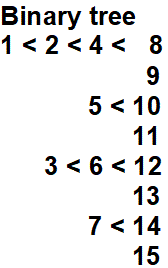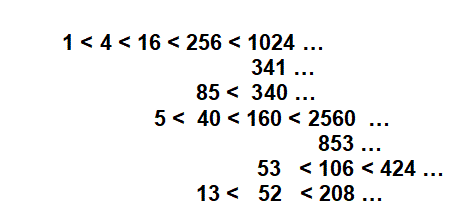I have a very simple proof of the Collatz conjecture. It only uses basic high school math. How can this be so, for a problem that has resisted a proof for nearly 90 years? I can only conclude that there must be some flaw but I can’t see a problem with it. Please point out any issues that you can find.
Much work has been done to research possible cycles of integer values that follow the Collatz rules. If such a cycle exists apart from the termination loop 1 > 4 > 2 > 1 then the conjecture would be false. Absence of such a cycle offers hope that the conjecture may be true but will never prove the conjecture true if tested for finite ranges. To prove the conjecture is true we must show that cycles are absent for all positive integers and that divergent growth is also absent for all positive integers.
We will build a tree of all possible orbits or paths to 1 as a topological directed graph. This will be shown to a) contain all positive natural numbers and b) be fully connected using a proof by induction. A simple proof exists for the Collatz conjecture. (several, in fact) These proofs avoid Baker’s theorem and prove a connected tree, and the absence of cycles and divergent growth follows. There are four main parts to the proof.
Outline
Part 1 Branch properties, branch types, completeness, terminal loop, type 3 bare branches, nodes on type 1 & 2 branches, spaced with fillers, uplinks and downlinks, branch types cycle. A general development of properties of branches.
Part 2 Colinked branch sets (a set of branches that link to all nodes on a single branch) connect only to type 1 & 2 branches, 4k+1 separation of terms, branch types cycle within a colinked set.
Part 3 The Binary tree has the same branch structure as the Collatz tree, as it also has the division rule, but connects by N-1 in place of the 3N+1 link that Collatz uses. Proof by induction is possible using monotonicity by term value and grid position. It Is a simple model for the Collatz system.
Part 4 Induction. Compressing a tree of type 1 and 2 branches, isomorphism with a binary tree, proof by induction using binary tree grid as a monotonic path, inflating the tree, Proof complete.
Please tell me to stop if I am out of order or not relevant. I do not want to takeover the site, but this approach seemed so obvious to me, and I cannot see any flaw in the argument. Once this is complete, I have two other different approaches by other methods. It seems to me that this is a very easy problem and I do not understand why no proof has appeared to date.
Definition of terms
1 Rule 1 is the division rule for even numbers. N/2.
2 Rule 2 is the tripling rule for odd numbers. 3N+1.
3 Rule 3 is the binary tree’s linking rule. N-1.
4 A branch is an odd positive integer followed by an unbounded set of doubling even numbers.
5 A root is the odd first term on a branch.
6 A node is the result of applying rule 2 or rule 3 to an odd root. 3N+1 for the Collatz system or N-1 for the binary system.
7 A tree is a set of branches connected by either the Collatz rule or the binary rule.
8 A filler is an even number that is not a node. They are 3N or 3N+2 in the Collatz system.
9 A branch type is the root mod 3 value of a branch but root ≡ 0 are labeled type 3.
10 A colinked branch set is a set of branches that link to all the nodes on a type 1 or type 2 branch in the Collatz system. They have a separation of 4k+1 and cycle branch types.
Defining branch structure for a tree.
Theorem 1: The division rule generates a branch structure.
Proof:
An even number on a branch has a form R2^k where R is the root of the branch.
Each use of rule 1 will remove one factor of 2.
No other odd factors are removed.
After k applications of the rule, all factors of 2 are removed and the odd root is reached.
All terms on a branch are a multiple of the root.
Application of rule 1 provides an orbit down a branch to the root.
Q.E.D.
Theorem 2: The set of branches contains every positive integer exactly once.
Proof:
Every positive odd number is the root of a branch with unique prime factors by the fundamental theorem of arithmetic.
If we multiply the set of all positive odd numbers by the set of all integer powers of 2, we may generate each positive integer in one unique way.
{1, 3, 5, 7, 9, 11, 13 …} * {1, 2, 2^2, 2^3, 2^4, 2^5, 2^6 …}
Every odd integer is represented as the root of a different branch.
Every even number has the format R2^k where R is the product of an integer’s odd prime factors and k is a count of the number of factors of 2.
Every integer is represented and has one specific location k on one branch.
No integer can appear in more than one location.
Q.E.D.
A termination loop exists.
Theorem 3: Branch 1 links to itself with a termination loop.
Proof:
In the Collatz tree the 3N+1 rule links a root of a branch to an even node.
The root R is odd.
The following two terms on a branch are 2R and 4R.
Tripling an odd root will give an odd result with a value between 2R and 4R.
Adding 1 will give an even number on the same branch only if:
3R+1 = 4R
Solving gives R = 1.
Only branch 1 can link to itself.
Q.E.D.
Theorem 4: Type 3 branches have no connection nodes.
Proof:
In the definition of a branch each term was double its predecessor.
Each term on the branch contains all the prime factors of the root.
Branches of 3N format have terms that are all a multiple of 3.
Therefore, they have no terms of 3N+1 format and are node free.
Q.E.D.
Theorem 5: 3N+1 nodes alternate with 3N+2 even filler numbers.
Proof:
A term of 3k+1 format on a branch, when doubled gives a result 6k+2.
This is equal to 2 modulo 3.
Doubling 3k+2 again gives 6k+4 which has a modulo 3 value of 1.
The root of the branch will follow the same mod 3 format but will be odd.
Q.E.D.
Corollary:
Any branch with a 3N+1 node has infinitely many such nodes, separated by a 3N+2 filler even number that is not a node and must be on a branch with a 3N+1 or 3N+2 root type as this is doubled to get the first even term.
Theorem 6: Type 1 branches have only downlink nodes.
Proof:
A type 1 branch has a root of 3N+1 format. The root mod 3 value is 1.
The first even number is a 3N+2 filler and is not a connection node.
The second even number is a 3N+1 node as type 1 and 2 branches alternate these values.
The branch linking to a node at the second even number by a 3N+1 link will have two rule 1 divisions by 2 that will reduce the value to (3N+1)/4 to reach the root. The result is a term about 75% of the linking branch root.
All higher nodes will have more rule 1 options and all following links to nodes are also downlinks.
Q.E.D.
Theorem 7: Type 2 branches have one uplink node.
Proof:
A type 2 branch has a root of 3N+2.
It will be followed by an even number of 3N+1 format, and the first node is immediately following the root.
A branch linking to this first node by 3N+1 will require only one rule 1 division by 2 to reach the root.
The connecting child branch has reached a parent branch with a root value of (3N+1)/2 which is an increase of about 50%. It is an uplink to a branch of higher root number.
All following nodes will have at least three rule 1 divisions available and will be downlinks.
Type 2 branches have one uplink site immediately following their root and all other connections are downlinks.
Q.E.D
Uplinks and downlinks
The only uplinked connections to a higher branch number are branches of 4k+3 format that link to the first node on a type 2 branch. A 4k+3 format branch links by 3N+1 to a 12k+10 node. A single division by 2 reaches a 6k+5 odd branch root. All other nodes have at least two division rule links that reduce the node to a value that is 4 times smaller than the node, and this is less than the 3N+1 increase except for the termination loop on branch 1.
All connection nodes exist on type 1 and type 2 branches. No nodes exist on type 3 branches as all terms are multiple of 3. Consecutive branches cycle as triplets of type1, type 3, and type 2 branch types.
This completes part 1, the structure of branches and node distribution. Part 2 looks at connections to nodes.