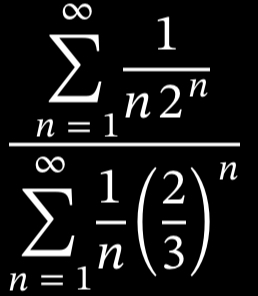Finding a specific irrational number

General
1

As I explained previously, I am working with a variant of 3n+1 where it is trivial to show that apart from a handful of numbers all orbits diverge. It goes as such:
f_a(2k) = 3k
f_a(2k+1) = 3k+a

I am interested in the trajectories of numbers. What I mean by a trajectory is the sequence of parities generated by it. For exemple, the trajectory of 2 under f_0 is: 01111… because f_0(2)=3, f_0(3)=3, and the trajectory of 4 is 0010011… (4->6->9->12->18->27->39…)

I proved earlier that numbers with diverging orbits (such as the one of 4 under f_0) have ultimately aperiodic trajectories.
It is tempting to see something like 0010011… as binary “decimals”, that would correspond to some irrational number between 0 and 1. My question is as follow: can you find any example of a triplet (r,a,s) such that the trajectory of r under f_a corresponds to the binary “decimals” of the irrational s ?

1 Like
2

Right! Or for any tricot f, for that matter. Good to try for a specific f first.

3

Hm, so the trick here seems to be defining the s in some way which is not just “the s induced by f_a^n(r)”. Is that correct?

What I mean is that for all sufficiently large r, we know that f_a(n) > n for all n \ge r and thus we know that r diverges and so the parity sequence is non-cyclic, so that corresponds to an irrational number. Thus for all such r,a there exists a corresponding s. But the difficulty comes in trying to define it in a more natural way (like saying that it is \pi or something like this?)

This seems very hard.

1 Like
4

You’re correct. That wouldn’t be very useful…

Anyway, I know it looks hard but note I am not asking about finding s for a given couple (a,r). If you want to start with s and find a and r that yield to that s, it would already be way better than what I have as currently I don’t even know how to start.

1 Like
5

Your problem looks interesting. To see how hard it is, we may reason as follows: Assuming that r and a are integers, the set of couples (r,a) is countable, and so is the number of admissible s. By picking an irrational s at random like \log 2, the chances that there exists a couple of integers (r,a) for that particular s are almost zero.

I’d say that finding a solution is hopeless, unless there is some kind of pattern in the digits …

6

Except you are not supposed to (and can’t, anyway) pick s at random. You will pick it from the countable set of computable numbers.

7

Go @Failix ! Here’s a quote from The Unreasonable Effectiveness of Mathematics in the Natural Sciences:

"There is a story about two friends, who were classmates in high school, talking about their jobs. One of them became a statistician and was working on population trends. He showed a reprint to his former classmate. The reprint started, as usual, with the Gaussian distribution and the statistician explained to his former classmate the meaning of the symbols for the actual population, for the average population, and so on. His classmate was a bit incredulous and was not quite sure whether the statistician was pulling his leg. “How can you know that?” was his query. “And what is this symbol here?” “Oh,” said the statistician, “this is pi.” “What is that?” “The ratio of the circumference of the circle to its diameter.” “Well, now you are pushing your joke too far,” said the classmate, “surely the population has nothing to do with the circumference of the circle.” "

But of course inside number theory, even Brun’s constant seems unrelated to all the other constants…

8

I already have some kind of results. Nothing revolutionizing (yet!) but still.

Considering the tricot T(2k->Nk, 2k+1->Nk+A):
traj(0,T) = [0] (0 repeating)
traj((N-2A)/(N-2)) = [1]
traj(x) is the complement of traj((N-2A)/(N-2) - x) (meaning you get one by taking the other and replacing 0s with 1s and 1s with 0s)

9

I have something cool about periodic trajectories. Considering the same tricot, to find for example trajectory [0001101110] you can do as follows:

  • get the length L of the period (here it’s 10)
  • consider the vector [N^(L-1) ; N^(L-2)2^1… ; N^(L-1-i)2^i … ; 2^(L-1) ] and sum all the terms that correspond to 1s in your period. Here that’s N^6*2^3 + N^5*2^4 + N^3*2^6 + N^2*2^7 + N^1*2^8.
  • multiply this by (N-2A)/(N^L-2^L)
  • you get the number that generates the trajectory you want!

The proof isn’t even complicated.

10

Awesome, @Failix, I would love to see your tricot for this example.

I’m inspired to try to recreate what you’ve done in (non-tricot) 3n+q style:

v = 0001101110
k = 10 (length of v)
x = 5 (number of odds in v)
d = 2^k - 3^x = 781
\beta(v) = 2^3 3^4 + 2^4 3^3 + 2^6 3^2 + 2^7 3^1 + 2^8 3^0 = 2296

Then 2296 should now cycle under the (grandiose-sounding) 3n + 781 rule, which it does:

2296 - 1148 - 574 - 257 - 821 - 1622 - 811 - 1607 - 2801 - 4592 - 2296

I wonder if this method is similar to yours …

11

For my example I used
(N 0 )
(N A )
In other words: 2k->Nk ; 2k+1 → Nk+A
N has to be odd, A can be any integer.

Of course, if you pick A at random, sometimes your result won’t be an integer.
For example, with N=3, A=0
(N-2A)/(N^L-2^L) = 3/(3^10-2^10) = 3/58025
N^6*2^3 + N^5*2^4 + N^3*2^6 + N^2*2^7 + N^1*2^8 = 13368
and 13368*3/58025 isn’t an integer
But you can always pick A in a way that works, at worse you can take A=(N-N^L+2^L)/2 so that (N-2A)/(N^L-2^L)=1 (sometimes there is a less greedy A that also works).

Now, to find a link with your method…
(I think you have a typo. 257 should be 574/2=287, but the rest seems good)
I also used this quite a while ago to find cycles but β isn’t a very nice function to work with. It made me, somehow, discover by myself the formula for the Moebius inversion (which I think is pretty cool) but after that I was kinda stuck.

When comparing the cycles:
Let’s say I take N=3, A = (N-N^L+2^L)/2 = (3-3^10+2^10)/2 = -29011
under (2k->3k ; 2k+1 → 3k-29011),
13368 → 20052 → 30078 → 45117 → 38663 → 28982 → 43473 → 36197 → 25283 → 8912 → 13368

If I take N=1, A = (N-N^L+2^L)/2 = (1-1^10+2^10)/2 = 512
N^6*2^3 + N^5*2^4 + N^3*2^6 + N^2*2^7 + N^1*2^8 = 8+16+64+128+256 = 472
under (2k->k ; 2k+1 ->k+512),
472 → 236 → 118 → 59 → 541 → 782 → 391 → 707 → 865 → 944 → 472

under (2k → k ; 2k+1 → 3k+392) (same as 3n+781 rule),
2296 → 1148 → 574 → 257 → 821 → 1622 → 811 → 1607 → 2801 → 4592 → 2296

If we manage to find a way to map (13368,472) to 2296, (20052,236) to 1148, (30078,118) to 574, etc, my gut feeling is that it would be huge.

1 Like
12

In my quest to find a specific irrational that would correspond to a specific trajectory, I am looking for the conditions to instantiate the trajectory: 110100100010000…
After quite a lot of calculations I figured I need N such that for all i big enough, N^i congruent 1 mod 2^(i+2)
That works for N=1, but does that work for other values of N? My guts tell me no but I am having a hard time proving it.

13

I think I got this, using Manea’s Lemma. Sadly the conclusion is that there is no way to generate this specific trajectory on an homogeneous tricot of height 2 (meaning there exists N and A such that 2k->Nk and 2k+1->Nk+A).

The proof goes as follows:
suppose we have x_0 whose trajectory is 1101001000…
x_1 whose trajectory is 101001000…
x_2 whose trajectory is 100100010000…
etc.

Then you have for any i: x_(i+1) = (1/2)^(i+1) * ( (2A-N)N^i + x_i*N^(i+1) ) (1)
We need all those to be integers, so we need that (2A-N)N^i + x_i*N^(i+1) = 0[mod 2^(i+1)]
N and 2^(i+1) are coprime so that’s equivalent to (2A-N)+Nx_i = 0[mod 2^(i+1)]
or (N-2A) = Nx_i [mod 2^(i+1)]

That means there exists k such that Nx_i = (N-2A)+k2^(i+1)
Replacing in (1): (EDIT: here is the error that makes that proof wrong)
x_(i+1) = (1/2)^(i+1) * ( (2A-N)N^i + N((N-2A)+k2^(i+1)) )
= (1/2)^(i+1) * ( (N-2A)(N-N^i) ) + Nk
For that to be an integer, we need (N-2A)(N-N^i) = 0 [mod 2^(i+1)]
but the only factor that can be even is (1-N^(i-1)), so we need N^(i-1) - 1 = 0 [mod 2^(i+1)]
so v_2(N^(i-1) - 1) >= i+1 (v_2 being the 2-adic valuation)
But through Manea’s lemma, if i is even, v_2(N^(i-1) - 1) = v_2(N-1)
so v_2(N-1) >= i+1
As we can take an even i as big as we want, that means v_2(N-1) is infinite, so N-1 is 0.
thus N=1
But if N=1, then our tricot only has ultimately periodic trajectories, which contradicts the premise.

1 Like
14

I like the irrational sequence you tried to create, though. I wonder if log_2(3) might be a good target … it keeps coming up in Collatz world.

15

I am not familiar with how to compute logarithms. How do you get it?
In binary, at first glance I’d do log(11) = log(10*1.1) = log(10)+log(1.1) = 1+log(1.1)
So the result would be 1.something… which isn’t precise enough.
Do you know of and algorithm I could take inspiration from, perhaps to build a recurrence?

EDIT: I think I found something: log(1.1) = (1/10)log(1.1^10) so I’d get it by successively squaring. The recurrence isn’t obvious yet but I’m working on it.

16

Good point. It’s the x where 2^x = 3 … but agreed that 2 to a non-integer is already a mind-bender. I mean, clearly it’s between 1 and 2, but yeah. Also occurring frequently is its reciprocal, 0.63093\ldots, which in binary is 0.1010000110000100100111001100000110101001101010011110100101001110000001000011111010101111011101111001000111110101001000010100001000001001000010100100100011011101101100001101111000110011110001010111000001110100101000010010001110111101100101110001001100101010\ldots

IMG_8231
IMG_8231258×296 20.8 KB

or maybe \sqrt{2} has some simpler series or continued fraction.

17

I didn’t have much luck trying the binary development of log2(3), but I noticed something interesting.
Actually, the proof I had that the trajectory 110100100010000… is impossible can also disprove the existence of any trajectory that contains an arbitrary large number of zeroes in succession.

To formulate it differently, for any number x on any homogenous tricot T, there is n such that x never hits a multiple of 2^n.
That n might be big (for 2 on 2k->3k ; 2k+1->3k+2, that’s at least 17), but it is finite.

Also, as a consequence of another property of homogenous tricots, it means the same is true for arbitrary long sequences of ones.

To me, it looks like a new exciting result, am I missing something?

1 Like
18

@Failix I’m not up on my tricot terminology – what’s a homogenous tricot? Is the tricot version of 5n+1 homogenous?

19

I mean the affine coefficient is the same on every line (so 2k->5k ; 2k+1 → 5k+3 is homogenous but not 2k->k ; 2k+1->5k+3)

20

So, for example if we stick to (2k->3k ; 2k+1->3k+2) (basically “reduced collatz except you still multiply by 3 even when the number is even”), for any nonzero starting number s there is a bound B(s) such that s never hits a multiple of 2^(B(s))
And for any s different from -1, there is a bound B’(s) such that s never hits a number congruent to -1 mod 2^(B’(s)).

Obviously, if x hits y, B(x)>=B(y) and B’(x)>=B’(y).

Would there be a way to calculate B(s)? By just running a computer we can tell that the trajectory of 2 eventually (after millions of steps) hits a sequence of 17 zeroes, so B(2)=B(3)=B(5)=… >=17.
17 is a lower bound, is there a way to get an upper bound?

Assuming we had a way to find B(s), we would get that s eventually hits some (2k+1)2^(B(s)-1), ie there is a n such that s(3/2)^n+sum((3/2)^i) = (2k+1)2^(B(s)-1) (where i walks over all the steps such that T^1(s) is odd)
=> s3^n+sum(3^i*2^(n-i)) = (2k+1)2^(B(s)-1+n)
=> s = ((2k+1)2^(B(s)-1+n) - sum(3^i*2^(n-i))) / 3^n = ((2k+1)2^(B(s)-1+n)3^(-n) - sum(3^(i-n)2^(n-i)) = ((2k+1)(2/3)^n*2^(B(s)-1) - sum((2/3)^(n-i))
I don’t know if one of those expression is more helpful than another, that’s pretty much where I am so far.

1 Like